O hablando en plata, cada término es la suma de los dos anteriores; siendo los dos primeros el cero y el uno respectivamente. De manera que los términos de la serie son:
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
La razón áurea es una proporción conocida desde la antigüedad. Se dice que dos segmentos a y b están en razón áurea si la razón de la suma de los dos al mayor, es igual a la razón del mayor al menor:
Se representa con la letra griega phi, Ø, y su valor es:
Además de poder definirse de otras formas la razón áurea tiene propiedades bastante curiosas. Una de ellas nos permite expresar su valor, como el límite del cociente de dos términos consecutivos de la sucesión de Fibonnaci:
o esta otra, que permite calcular el n-ésimo término de la sucesión de Fibonnaci sin necesidad de conocer los anteriores
Una de las cosas que siempre me ha fascinado de las matemáticas es como se relacionan entre sí cosas que, aparentemente, son dispares.
De forma análoga a la razón áurea, se puede definir el concepto de ángulo, o arco, áureo.
En este caso:
Cambiando de tema, si tenemos un triángulo en el plano, el punto de intersección de las mediatrices de sus lados nos determina una circunferencia que pasa por los tres vértices. Al centro de dicha circunferencia (Q) se le denomina circuncentro
Supongamos que tenemos un conjunto de puntos distribuidos en el plano y los agrupamos de tres en tres (a este proceso se le denomina triangulación). Si todas las circunferencias circunscritas de cada uno de los triángulos formados, no contiene otros puntos aparte de los tres que la definen diremos la triangulación es una triangulación de Delaunay.
Conectando los centros de las circunferencias circunscritas se produce el diagrama de Voronoi (en rojo).
Supongo que si habéis llegado hasta aquí, os habréis ganado echar un vistazo
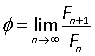
5 comentarios:
Si no he entendido mal, el diagrama de Voronoy se obtiene conectando los centros de la cicunferencias no de cualquier modo, cualquiera con cualquiera, sino el de cada circunferencia con los de las tres circunferencias circunscritas a los tres triángulos adyacentes al suyo...
Otra de las propiedades curiosas del phi este, por lo que he visto, es que su parte decimal es exactamente igual que la de su inverso.
Vanbrugh: Cierto. Gracias por la aclaración.
La demostración es fácil a partir de la definición de phi:
phi = 1 + 1/phi
P.D. ¿Alguien sabe cómo hacer para que aparezcan letras griegas en el texto?
Pegándolas del mapa de caracteres:
Ø = 1 + 1/Ø
(Igual que has hecho en el texto del post, me imagino).
Precioso video (y una definición de imagen espectacular).
Publicar un comentario